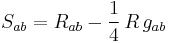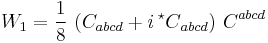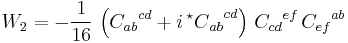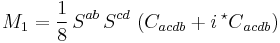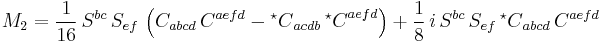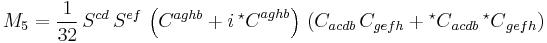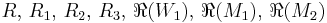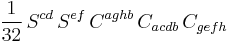Carminati–McLenaghan invariants

In general relativity, the Carminati–McLenaghan invariants or CM scalars are a set of 16 scalar curvature invariants for the Riemann tensor. This set is usually supplemented with at least two additional invariants.

1 Mathematical definition
2 Complete sets of invariants
3 See also
4 References
5 External links

Mathematical definition

The CM invariants consist of 6 real scalars plus 5 complex scalars, making a total of 16 invariants. They are defined in terms of the Weyl tensor 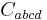$C_{abcd}$ and its left (or right) dual 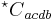${{}^\star C}_{acdb}$ , the Ricci tensor 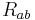$R_{ab}$ , and the trace-free Ricci tensor

$S_{ab} = R_{ab} - \frac{1}{4} \, R \, g_{ab}$

In the following, it may be helpful to note that if we regard 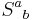${S^a}_b$ as a matrix, then 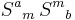${S^a}_m \, {S^m}_b$ is the square of this matrix, so the trace of the square is 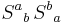${S^a}_b \, {S^b}_a$ , and so forth.

The real CM scalars are

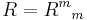$R = {R^m}_m$ (the trace of the Ricci tensor)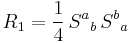
$R_1 = \frac{1}{4} \, {S^a}_b \, {S^b}_a$
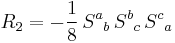
$R_2 = -\frac{1}{8} \, {S^a}_b \, {S^b}_c \, {S^c}_a$
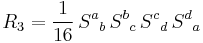
$R_3 = \frac{1}{16} \, {S^a}_b \, {S^b}_c \, {S^c}_d \, {S^d}_a$
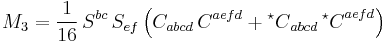
$M_3 = \frac{1}{16} \, S^{bc} \, S_{ef} \left( C_{abcd} \, C^{aefd} %2B {{}^\star C}_{abcd} \, {{}^\star C}^{aefd} \right)$
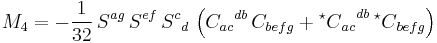
$M_4 = -\frac{1}{32} \, S^{ag} \, S^{ef} \, {S^c}_d \, \left( {C_{ac}}^{db} \, C_{befg} %2B {{{}^\star C}_{ac}}^{db} \, {{}^\star C}_{befg} \right)$

The complex CM scalars are

$W_1 = \frac{1}{8} \, \left( C_{abcd} %2B i \, {{}^\star C}_{abcd} \right) \, C^{abcd}$
$W_2 = -\frac{1}{16} \, \left( {C_{ab}}^{cd} %2B i \, {{{}^\star C}_{ab}}^{cd} \right) \, {C_{cd}}^{ef} \, {C_{ef}}^{ab}$
$M_1 = \frac{1}{8} \, S^{ab} \, S^{cd} \, \left( C_{acdb} %2B i \, {{}^\star C}_{acdb} \right)$
$M_2 = \frac{1}{16} \, S^{bc} \, S_{ef} \, \left( C_{abcd} \, C^{aefd} - {{}^\star C}_{acdb} \, {{}^\star C}^{aefd} \right) %2B \frac{1}{8} \, i \, S^{bc} \, S_{ef} \, {{}^\star C}_{abcd} \, C^{aefd}$
$M_5 = \frac{1}{32} \, S^{cd} \, S^{ef} \, \left( C^{aghb} %2B i \, {{}^\star C}^{aghb} \right) \, \left( C_{acdb} \, C_{gefh} %2B {{}^\star C}_{acdb} \, {{}^\star C}_{gefh} \right)$

The CM scalars have the following degrees:

$R$ is linear,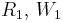
$R_1, \, W_1$ are quadratic,
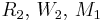$R_2, \, W_2, \, M_1$ are cubic,
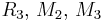$R_3, \, M_2, \, M_3$ are quartic,
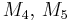$M_4, \, M_5$ are quintic.

They can all be expressed directly in terms of the Ricci spinors and Weyl spinors, using Newman–Penrose formalism; see the link below.

Complete sets of invariants

In the case of spherically symmetric spacetimes or planar symmetric spacetimes, it is known that

$R, \, R_1, \, R_2, \, R_3, \, \Re (W_1), \, \Re (M_1), \, \Re (M_2)$

$\frac{1}{32} \, S^{cd} \, S^{ef} \, C^{aghb} \, C_{acdb} \, C_{gefh}$

comprise a complete set of invariants for the Riemann tensor. In the case of vacuum solutions, electrovacuum solutions and perfect fluid solutions, the CM scalars comprise a complete set. Additional invariants may be required for more general spacetimes; determining the exact number (and possible syzygies among the various invariants) is an open problem.

References

Carminati, J.; and McLenaghan, R. G. (1991). "Algebraic invariants of the Riemann tensor in a four-dimensional Lorentzian space". J. Math. Phys. 32: 3135–3140. Bibcode 1991JMP....32.3135C. doi:10.1063/1.529470.

External links

The GRTensor II website includes a manual with definitions and discussions of the CM scalars.

Carminati–McLenaghan invariants

Contents

Mathematical definition

Complete sets of invariants

See also

References

External links